BALTRAD
1. Algorithm name
Dynamical downscaling of ground precipitation rate – DOWNSCALE
2. Basic description
a) Physical basis of the algorithm
Multiplicative cascade with weights’ determination by dynamic method is used. The cascade weights vary from grid to grid and in every time-step of downscaling process and depend on the spatial rainfall distribution. The weights are proportional to amount of rainfall in three nearest neighbouring larger-scale grids and the parent one.
b) Amount of validation performed so far
Prototype was developed and tested in the frame of RISK-AWARE Project (2003-2007).
c) References (names and contact information of all developers during the evolutionary history, scientific papers)
- IMGW, Department of Ground Based Remote Sensing.
- Scientific papers: Jurczyk, A., Ośródka, K., and Szturc, J., 2008. Research studies on improvement in real-time estimation of radar-based precipitation in Poland. Meteorol. Atmos. Phys., 101, 159-173.
3. ODIM metadata requirements for I/O
- Top-level what: object.
- Dataset-specific what: product, gain, offset, nodata, undetect.
4. Input data
a) What kind of radar data (including the list of previous algorithms and quality flags applied)
One of weather radar products that reflects ground precipitation rate RATE or accumulation ACRR as IMAGE or COMP files: PPI, CAPPI, PCAPPI, MAX, etc.
b) Other data (optional and mandatory, applying “universally” agreed formats, geometry)
None
5. Logical steps, using any of: text, flow charts, graphics, equations (or references to equations), conditional branches in “all possible cases”.
Multiplicative cascade is used o distribute rainfall on smaller-scale grids’ domain (Fig. 1). In the downscaling scheme the coarse-resolution rainfall grid is subdivided into 4 equal output grids with rain values set to the larger-scale rain value multiplied by cascade weights with the constraint that the total amount of rainfall must be preserved. The next assumption is that distribution (pattern) of precipitation in parent grid on four output pixels follows the pattern in the parent grid vicinity defined as 3 x 3 grids. The process is repeated several times until desired resolution is achieved.
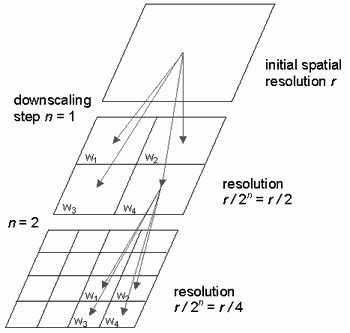
Fig. 1. Cascade approach for downscaling.
Downscaling is performed using the cascade approach with weights’ determination by dynamic method. The cascade weights vary from grid to grid in every step of downscaling process and depend on the spatial rainfall distribution. The weights are proportional to amount of rainfall in three nearest neighbouring larger-scale grids and the parent one.
For instance, if R5 is the parent grid (Fig. 2), then the dynamic weights are as follows:
The weights are normalised to preserve the total amount of rainfall:
Finally precipitation value in the smaller-scale output grid is set to the parent value multiplied by the relevant calculated weight:
The downscaled weights and precipitation values are calculated in each downscaling step for each grid of the rainfall map. The process is repeated until the desired resolution is achieved.
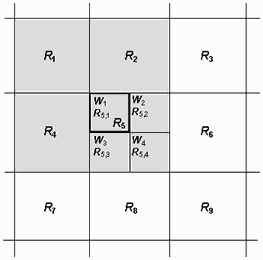
Fig. 2. Scheme of grid numbering in the dynamic method.
6. Output
a) Data type using ODIM notation where possible, e.g. DBZH
- Field of downscaled precipitation rate RATE or accumulation ACRR as IMAGE or COMP object.
- Quality index field QIND as IMAGE or COMP object.
7. Outline of a test concept exemplifying the algorithm, as a suggestion for checking that an implementation has been successful.
Downscaling tests were conducted radar data from August 2006 which was the rainiest month in this year. First the initial 1-km precipitation fields were upscaled using simple mean value into 2, 4, 8, 16 and 32-km fields. Then they were downscaled back into 1-km resolution fields and compared with the initial 1-km field. Additionally, for comparison, two simple downscaling methods were introduced: simple decomposition (where rainfall values of constituent smaller-scale grids are directly inherited from the parent larger-scale grid) and linear interpolation (rainfall values result from linear interpolation of the parent grid and neighbouring ones).
The quality of dynamic method was tested as a function of coarse resolution (2, 4, 8, 16, and 32 km). As it was expected the results strongly depend on the resolution. All characteristics get worse along with the increase of coarse resolution apart from BIAS which zero values result from the method assumption. The dynamic method was also compared against two simple downscaling methods (simple decomposition and linear interpolation). Downscaling effectiveness in terms of the RMSE, correlation coefficient R and mean absolute error MAE is shown in the diagrams in Fig. 3 for different coarse resolutions. It is noticeable that the dynamic algorithm slightly improved the rainfall field quality, which depends on the initial resolution.
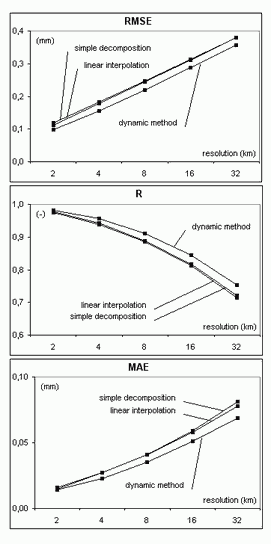
Fig. 3. Effectiveness of downscaling methods: dynamic one, simple decomposition, and linear interpolation, for different coarse resolutions 2, 4, 8, 16, and 32 km (initial 1-km field as reference).
In Fig. 4 one example of the performance of dynamic method is shown. The rainfall field with coarse 16-km spatial resolution was downscaled to 1-km resolution. As a reference the initial 1-km field is presented. Basing on statistical results, it can be concluded that rainfall pattern was reconstructed successfully. The algorithm reflected wet and dry grids quite well and the spatial variability of rainfall was correctly reproduced.
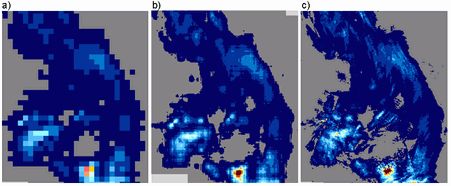
Fig. 4. Example of precipitation downscaling from 16 to 1-km resolution using dynamic method: (a) map of 16-km resolution, (b) downscaled to 1 km, and (c) initial 1-km map (29 August 2006, 06 UTC).