BALTRAD
1. Algorithm name
Retrieval of vertical profiles (reflectivity, wind speed, and wind direction) from polar volume data (WRWP)
2. Basic description
a) Physical basis of the algorithm
The algorithm is based on the VVP method.
b) Amount of validation performed so far
The dealiasing and wind profile algorithms have been been validated for two Swedish radar sites using radiosonde observations over a 18-month-period.
Haase, G., 2013: Validating Baltrad and Nordrad wind profile retrievals using radiosonde observations, 21 pages.
c) References (names and contact information of all developers during the evolutionary history, scientific papers)
The software has been developed by Günther Haase and Tomas Landelius (SMHI).
Haase G. and Landelius T., 2004: De-aliasing of Doppler Radar Velocities Using a Torus Mapping. J. Atmos. Oceanic Technol., 21, 1566-1573.
3. ODIM metadata requirements for I/O
nbins, nrays, gain, offset, nodata, undetect, rscale, elangle
4. Input data
a) What kind of radar data (including the list of previous algorithms and quality flags applied)
Polar volume or scan
b) Other data (optional and mandatory, applying “universally” agreed formats, geometry)
5. Logical steps
This algorithm derives vertical profiles of reflectivity, wind speed, and wind direction from polar volume data.
Assuming a uniform wind field the radial wind (V) has the form of a sine for constant range and elevation angle:
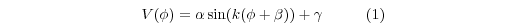
where φ is the azimuth angle. The four constants are amplitude ( | α| ), period (2π/k), phase shift (β), and vertical displacement (γ). The terminal velocity of the falling hydrometeors is implicitly included in γ. For k=1 Eq. (1) yields
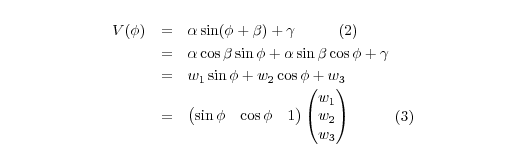
with
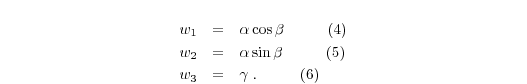
Equation (3) can be extended to n velocities which results in a nonhomogeneous matrix equation of the form:

For more than three independent measurements, i.e. n>3, Eq. (7) is an overdetermined linear system which can be solved using a QR factorization of A. The resulting values w1, w2, and w3 are utilized to determine α, β, and γ in Eq. (2). Squaring and adding Eqs (4) and (5) leads to
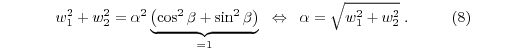
Solving Eq. (4) for α and inserting it into Eq. (5) results in
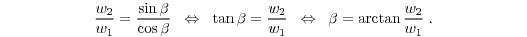
Finally, Eq. (6) provides an expression for the vertical displacement γ. Hence, Eq. (2) describes the radial wind model which is closest to the observations. The real wind velocity is identical with the amplitude ‘‘α_ in Eq. (8) while the wind direction is obtained from the derivative with respect to azimuth angle
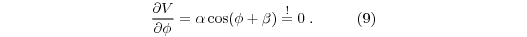
Hence, Eq. (9) equals zero for
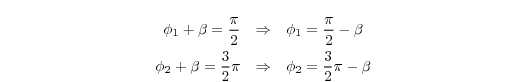
where φ1 and φ2 are the extreme values of Eq. (2). The second derivative of Eq. (2) with respect to azimuth angle is
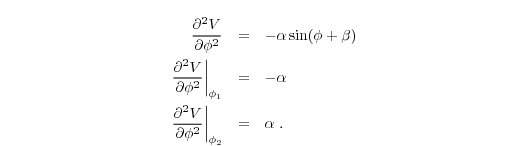
From Eq. (8) we know that α>0. Thus, the radial velocity in Eq. (2) has a maximum at φ1 and a minimum at φ2. Usually the wind direction is expressed in terms of the direction from which the wind originates (for example, a westerly wind blows from the west to the east). Furthermore, radial velocities away from the radar (outbound) are defined as positive while velocities towards the radar (inbound) are defined as negative. Therefore the wind direction in the specified height layer is given by φ2.
6. Output.
a) Data type using ODIM notation where possible, e.g. DBZH
dbz, dbz_dev, ff, ff_dev, dd, n (DBZH/VRAD)